Q-learning-sarsa-sarsa-lambda

强化学习三兄弟

哈喽，欢迎来到阿方小课堂，强化学习学的我晕乎乎的，下面我把自己这几天的理解收获整理一下，欢迎在评论区向我指出错误。

Q-learning与Sarsa

Q-learning是Off-policy（离线学习）,而Sarsa是On-policy（在线学习），他们的区别是，Sarsa 是说到做到型，即边做边学；而Q-Learning是说到但并不一定做到，其可以通过观察别人的经历来学习。二话不说，贴出伪代码

其中，r表的含义在这，假设我们的 Q(s, a) 是一个 Q table，如下图所示，该表格表示共有三个 state (状态)： S_1 、S_2、S_3 ,每个状态都有三个可选 action (动作) ：a_1、a_2、a_3 ，对所有的状态-动作以0赋值：

| Q(s,a) | a_1 | a_2 | a_3 |
| :——- | :—: | :—: | —-: |
| S_1 | 0 | 0 | 0 |
| S_2 | 0 | 0 | 0 |
| S_3 | 0 | 0 | 0 |

Q-learning 算法和 Sarsa 算法都是从状态s开始，根据当前的 Q table 使用一定的策略（ε - greedy）选择一个动作$a$，然后观测到下一个状态s’，并再次根据 Q table 选择动作a’。

可以看出更新 Q(s, a) 需要用到下一个状态的动作a’，而两种算法的不同点正是选取a’的方法不同。
根据算法描述，在选择新状态s’的动作a’时，Q-learning使用贪心策略(greedy)，即选取值最大的a’，此时只是计算出哪个a’可以使Q(s, a)取到最大值，然后更新Q table，并没有真正采用这个动作a’。贴出Q-learning更新Q table的代码。

for i in range(1000):
    # 对每一个训练,随机选择一种状态
    state = random.randint(0, 5)
    while state != 5:
        # 选择r表中非负的值的动作
        r_pos_action = []
        for action in range(6):
            if r[state, action] >= 0:
                r_pos_action.append(action)
        next_state = r_pos_action[random.randint(0, len(r_pos_action) - 1)]
        q[state, next_state] = r[state, next_state] + gamma * q[next_state].max()
        state = next_state

而 Sarsa 则是仍使用ε - greedy策略，并真正采用了这个动作a’。代码如下：

for i in range(100000):
    # 对每一个训练,随机选择一种状态
    state = random.randint(0, 5)
    while state != 5:
        # 选择r表中非负的值的动作
        actions = []
        for a in range(6):
            if r[state, a] >= 0:
                actions.append(a)
        # 采取动作
        action = actions[random.randint(0, len(actions) - 1)]

        R = r[state, action]
        next_state = action
        actions = []
        for a in range(6):
            if r[next_state, a] >= 0:
                actions.append(a)
        # 采取相同的动作（sarsa核心）
        next_action = actions[random.randint(0, len(actions) - 1)]
        q[state, action] = R + gamma * q[next_state, next_action]

        state = next_state
        action = next_action

Q-Learning因为有了 maxQ，所以也是一个特别勇敢的算法，原因在于它永远都会选择最近的一条通往成功的道路，不管这条路会有多危险。而 Sarsa 则是相当保守，它会选择离危险远远的。

Sarsa与Sarsa-lambda
Sarsa-lambda与Sarsa相似，都是On-policy，但是在每次take action获得reward后，Sarsa只对前一步Q(s,a)进行更新，Sarsa-lambda则会对获得reward之前的步进行更新。它到终点后会再反过来看一下自己曾经走过的路。

大体上与Sarsa相同，只是增加一个指标，这样可以使学习效率变高，能更快速的达到目的Q表。

这个指标就是在获取到最终奖励时，也可以说是到达最终目的地时，各个位置的不可或缺性。

表示方法：

先定义一个E表，用来记录经过的位置，每走一步，如果这个点不在E表中，则添加这个点到E表中，并将这个E(s,a)的值改为+1（还可以优化，下面说），如果表中存在这个位置，则直接更新这个位置的值，然后在走下一步之前对E表进行整体衰减。也就是说每走一步，就要对E表的当前位置的值进行刷新，然后再进行衰减。衰减的意义就在于如果一旦到达终点，就可以体现出来E表中各个位置对到达终点的不可或缺性。如果衰减比例为0，也就是每次都给E表里的值乘0，就意味着表里最后就剩下一个离终点最近的位置了，如果为1呢，则E表里的重复的越多的位置收益越大（so，这不合理，需要优化），所以，衰减比例应该取一个0~1之间的数比较合理。

E表的用法就是在Sarsa的基础上，每次更新的时候加上这个E表里对应位置的值就可以了。这就是传说中的Sarsa lambda了。下面说一下如何优化：

前面我们说每次经过这个某个位置，都把E表里对应值+1，这样对有些位置会很不公平，可能会出现离终点最近的那个位置的E值比中间的某个点的E值还要低，这很不科学。优化办法就是给E里的值定个上限，每次走到这个位置，就把他重新定为1，然后从1开始衰减，这样就不会出现上述的bug了。

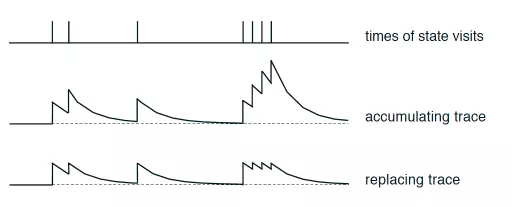
简单介绍一下图里的内容，第一行说的是某个位置出现和时间的关系；第二行说的是E值+1那个情况；第三行说的是定个上限为1的规矩。
总结
哇~强化三兄弟的介绍就这么结束了，对亏了简书，知乎，CSDN等论坛上的各路大神，贴上URL

https://zhuanlan.zhihu.com/p/29283927

https://blog.csdn.net/u010089444/article/details/80516345

https://www.jianshu.com/p/91fbc682fb3e

安呐~

强化学习三兄弟

Q-learning与Sarsa

Sarsa与Sarsa-lambda

总结